Relevance Vector Machine Learning for Bayesian Linear Regression

Relevance Vector Machine (RVM) is a sparse Bayesian learning technique and provides probabilistic estimates of model parameters. Different modeling challenges including noisy data, overfitting, the curse of dimensionality, small experimental datasets exist. Thus, Bayesian relevance learning addresses these challenges and provides many advantages.

Consider a linear regression forward problem as follows: \(\mathbf{d} = \mathbf{K} \boldsymbol{\theta} + \boldsymbol{\eta}\).

Here, the noise \(\boldsymbol{\eta}\) is assumed to be Gaussian independent and identically (i.i.d.) random vector, \(\mathbf{K}\) is the kernel, \(\boldsymbol{\theta}\) are the unknown stochastic model parameters to be estimated and \(\mathbf{d}\) is the experimental data.

The probabilistic formulation of the problem is as follows:

where \(\mathbf{\Gamma_d} = \Delta^2 \mathbf{I}\) representing the uncertainties on the observed parameters.

Prior \(\boldsymbol{\theta} \sim \mathcal{N}(\mathbf{0},\delta^2)\)

Prior variance \(\delta^2 \sim \text{Gamma}(\alpha_{\delta}, \beta_{\delta})\)

Data noise variance \(\Delta^2 \sim \text{Gamma}(\alpha_{\Delta}, \beta_{\Delta})\)

The joint posterior probability can be written as follows:

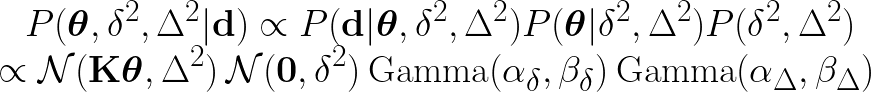
The goal is to estimate the model parameters \(\boldsymbol{\theta}\) which maximizes the joint posterior probability distribution. Here, both prior and data noise variances are considered random variables, which leads to hierarchical relationship. Thus, this probabilistic approach is termed as hierarchical/multilevel Bayesian and is different than the traditional Bayesian method.

[More details coming soon.]

References:

1. M. E. Tipping. Sparse bayesian learning and the relevance vector machine. Journal of Machine Learning Research, 1(3):211–244, 2001.

2. C. M. Bishop. Pattern Recognition and Machine Learning. Springer, New York, 2006.