SAYALI KEDARI

I am currently a SIMULIA Services Industry Process Consultant at Dassault Systemes.

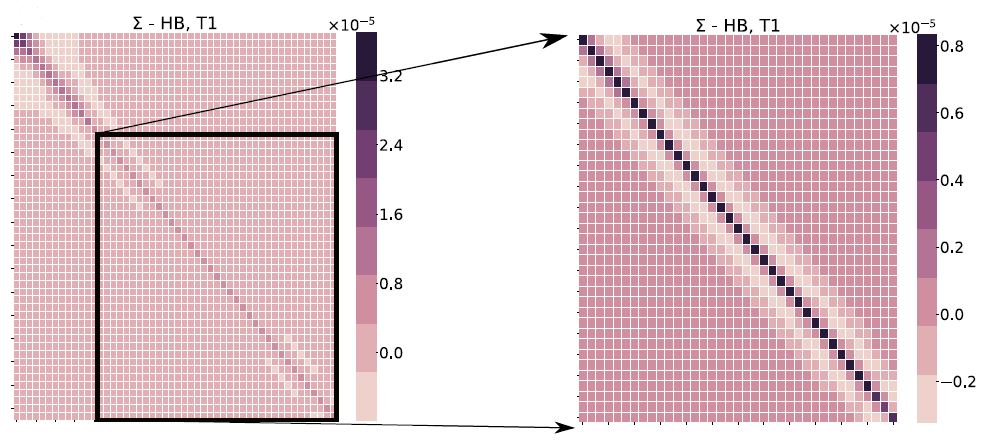
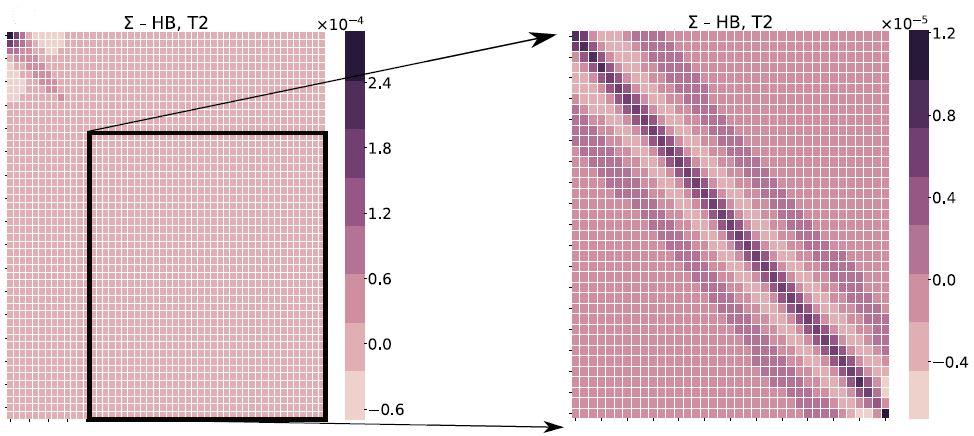
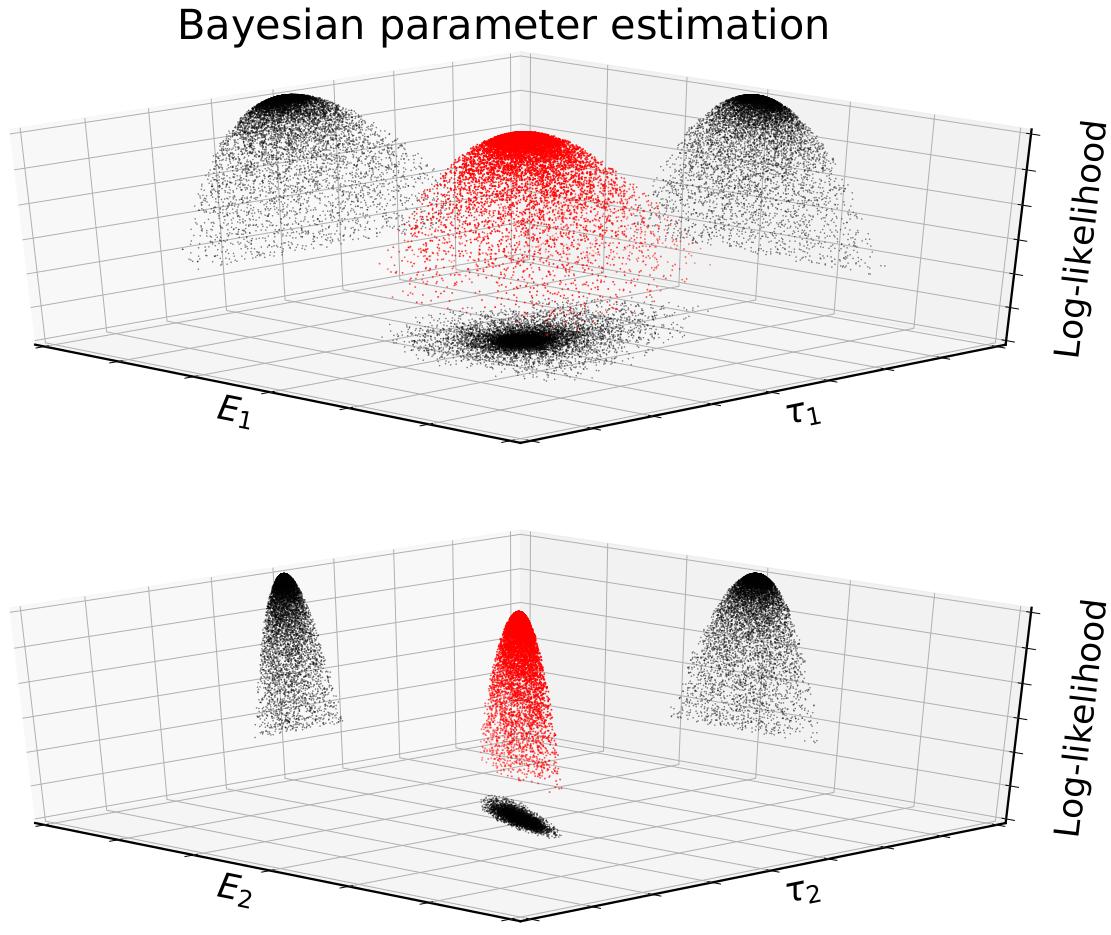
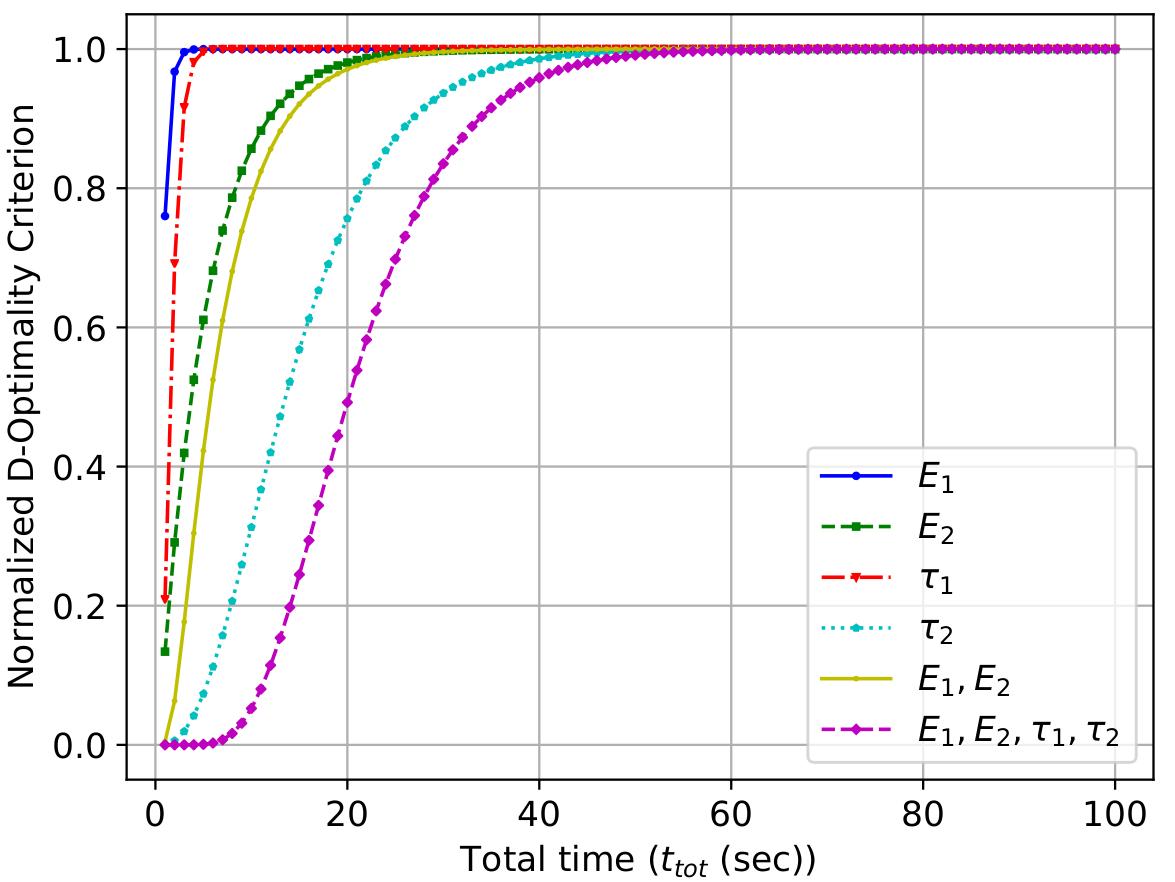
I earned my Doctor of Philosophy (Ph.D.) in mechanical engineering in the spring 2022, advised by Prof. Kumar Vemaganti at the University of Cincinnati. My Ph.D. research is focused on Bayesian learning in computational rheology - applications to soft biological tissues and polymers, an area that is highly computational and involves multiple disciplines of study including Bayesian statistics, mechanical engineering and scientific computing. My Ph.D. work involved investigating rheological constitutive models of solids (soft biological materials and polymers), applying Bayesian statistical approaches to analyze the mechanical behavior of solids in order to improve the reliability of computer model predictions in real-world applications (crash-induced traumatic brain injury, tissue engineering, computer-aided surgery, soft robotics, baby- and feminine-care absorbent articles, running shoes).

I worked on research projects in collaboration with Procter & Gamble (P&G) at the UC Simulation Center. My work involved employing physics-based predictive-design-approach and developing digital twins to drive and outline process design and optimization guidelines using commercial finite element analysis (FEA) and programming tools.

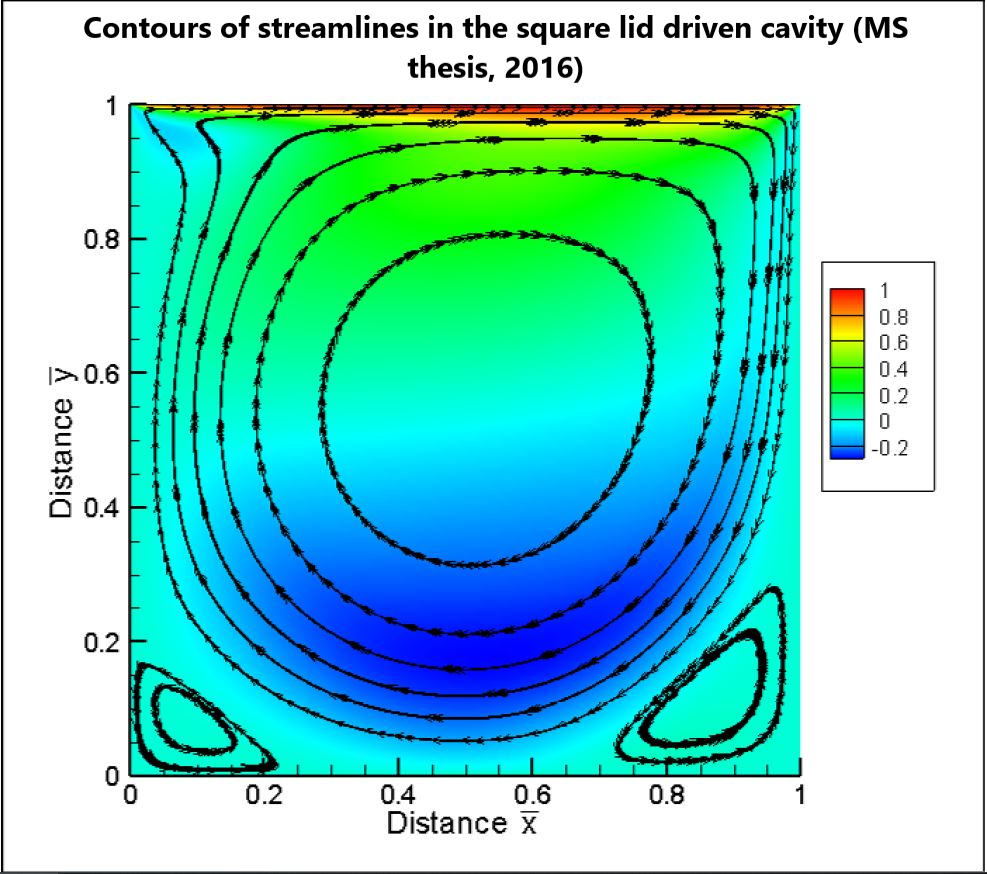
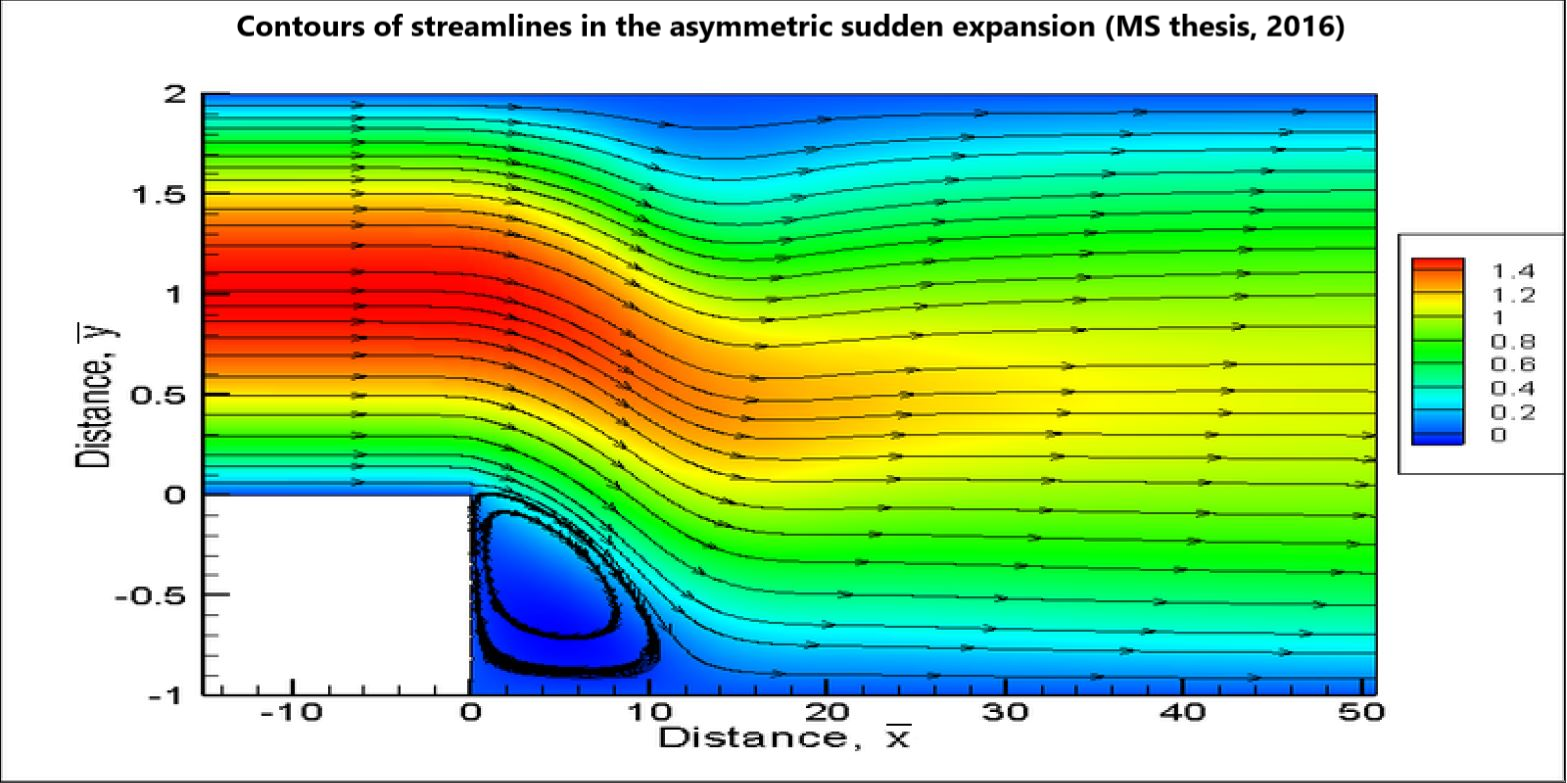
I earned my Master of Science (M.S.) in mechanical engineering in 2016 from the University of Kansas, where my research was focused on finite element analysis and computational fluid mechanics (Computational Mechanics Laboratory).

Resume: pdf

Contact: kedarisa [at] mail [dot] uc [dot] edu

Summary

• Strong background in finite element analysis and scientific computing.
• Comprehensive programming skills in Python, Julia, C++, C, MATLAB languages, frameworks such as scikit-learn; and extensive experience with commercial CAE tools such as Abaqus.
• Demonstrated ability to work both independently as well as collaboratively as a member of cross-functional teams in industry and academia.
• Authored 4 peer-reviewed journal publications.
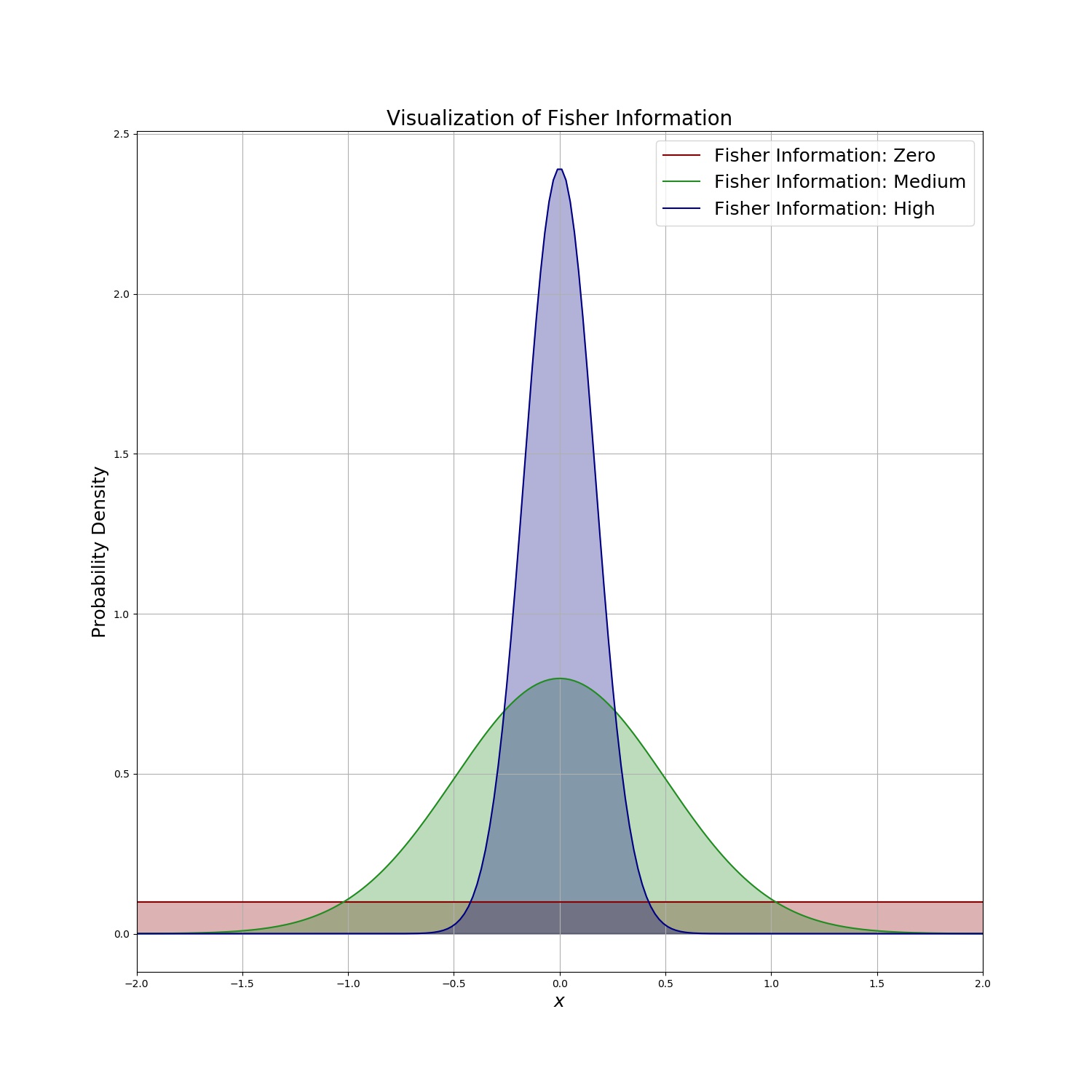
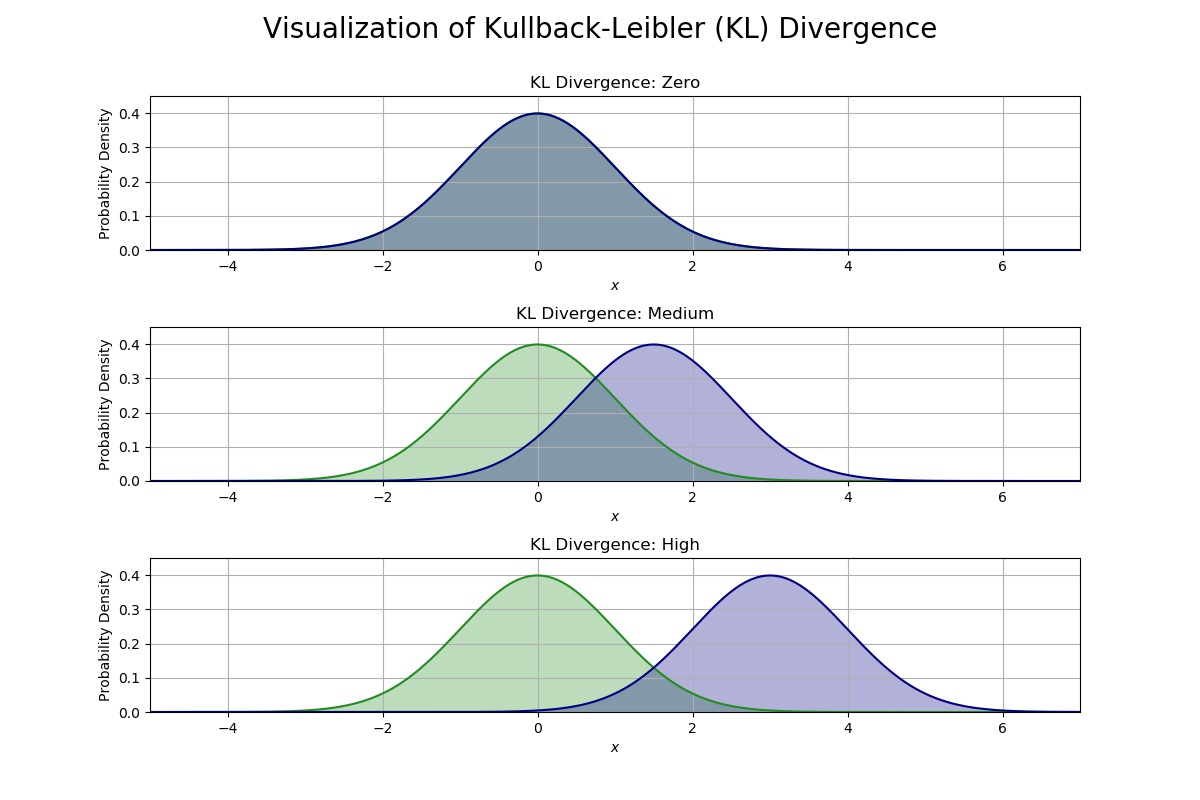
• Expertise in different aspects of uncertainty quantification including optimal experimental design and calibration.
• Experience in the application of the Bayesian framework to solve probabilistic inverse problems and traditional optimization methods to solve deterministic inverse problems in solid and fluid mechanics.
• Proven ability to effectively handle multiple projects concurrently and manage competing priorities under demanding deadlines.

Research Interests

Solid mechanics, scientific computing, finite element analysis, uncertainty quantification, machine learning.

Teaching

• MET 4076 - Applied computational methods, spring and summer 2018.

Travel

I like to travel and share my experiences. You can read about some of my trips at my travel photography blog.

Bayesian posterior covariance matrix with T1 regularization, Kedari et al., A hierarchical Bayesian approach to regularization with application to the inference of relaxation spectra, 2021	Bayesian posterior covariance matrix with T2 regularization, Kedari et al., A hierarchical Bayesian approach to regularization with application to the inference of relaxation spectra, 2021
Bayesian parameter estimation (PhD dissertation), Kedari, Bayesian Learning in Computational Rheology: Applications to Soft Tissues and Polymers, 2022	D-optimality criterion, Vemaganti et al., On the Inference of Viscoelastic Constants from Stress Relaxation Experiments, 2019
Contours of streamlines in the square lid driven cavity (MS thesis), Kedari, Investigation of More Complete Constitutive Theories for Heat Conduction in Solids and for Deviatoric Stress Tensor in Incompressible Fluids, 2016	Contours of streamlines in the asymmetric sudden expansion (MS thesis), A nonlinear constitutive theory for deviatoric Cauchy stress tensor for incompressible viscous fluids, 2017